Les milieux magnétiques et les Milieux diélectriques présentent beaucoup d'analogies.
Les principales différences sont:

• On parle d'aimantation \(\vec M\) et de \(\vec H\) pour désigner l'induction magnétique
• La susceptibilité magnétique \(\chi_m\) peut prendre toutes les valeurs. (Susceptibilité électrique)

Définitions

Moment magnétique
Aimantation

Champ magnétique

L'analogie avec les Milieux diélectriques apparaît quand on pose \(\vec m={{\vec p}}\) (\(\vec p\): Moment dipolaire) et \(\mu_0={{\frac 1\epsilon_0}}\)

Champ magnétique créé par un dipôle

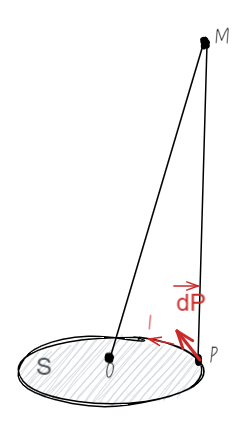
Le champ magnétique du dipôle, dans l'Approximation dipolaire, est:
$$\vec B=\frac{\mu_0}{4\pi}\left[-\frac{\vec m}{r^3}+3\frac{\vec r(\vec m.\vec r)}{r^5}\right]$$
Avec:

• \(\vec m\): le Moment magnétique, ici \(\vec m=I\vec S\)

Energie potentielle d'un moment magnétique

L'expression de l'énergie potentielle nous dit que les dipôles vont tendre à s'orienter dans le sens du champ magnétique extérieur.
L'énergie potentielle d'un moment magnétique plongé dans un champ magnétique extérieur est:
$$\vec E_P={{-\vec m.\vec B_{ext} }}$$
Avec:

• \(\vec m\): le Moment magnétique

Aimantation d'un milieu

Le fait que le milieu soit aimanté est équivalent équivalent à avoir un milieu parcouru par \(2\) courants d'aimantation:

1. Courant volumique d'aimantation:

$$\vec j_M={{\vec {rot}(\vec M)}}$$

1. Courant surfacique d'aimantation:

$$\vec {j}_{S,M} ={{\vec M\wedge\vec n}}$$
Avec:

• \(\vec n\): le vecteur normale à la surface
• \(\vec M\): l'Aimantation

Remarque: Les courants d'aimantation ne sortent pas du milieu magnétique

Equation de Maxwell

Equations de Maxwell (Dans un milieu magnétique)

Susceptibilité et excitation magnétique

Susceptibilité magnétique
Perméabilité d'un milieu

Relations de passages

Relations de passage du champ magnétique dans un milieu magnétique

Les relations de passages pour le champ magnétique dans un milieu magnétique sont:
$$\vec{n}_{1\to 2}.(\vec B_2-\vec B_1)={{0}}$$
$$\vec{n}_{1\to 2}\wedge(\vec H_2-\vec H_1)={{\vec j_{S,l}}}$$

Théorème d'ampère

Théorème d'Ampère (Forme générale)

Energie magnétique

Energie volumique magnétique

Dans un milieu magnétique, l'énergie volumique magnétique est:
$$u_m={{\frac 12\vec H.\vec B}}$$

Interprétation microscopique

Moment cinétique orbital

En mécanique classique:
On suppose qu'un électron (masse: \(m_e\), charge: \(-e\)) possède une orbite circulaire autour du noyau
Le moment cinétique orbital: \(\vec \Gamma_0=\vec r\wedge (m\vec v)\)
\(I=\frac eT\) avec \(T\) la période de révolution de l'électron
Le moment magnétique: \(\vec m=\frac I2\oint \vec r\wedge \vec{dl}\) avec \(\vec {dl}=-\vec v dt\)
Dans le cas d'une force centrale: \(\vec \Gamma_0=constante\)
Donc: \(\vec m=\frac{-I}{2}\vec r\wedge\vec v\int_0^Tdt\)
$$\vec m=-\frac e2\frac{\vec \Gamma_0}{m_e}$$
On définit le facteur gyromagnétique de l'électron: \(\gamma=-\frac{e}{2m_e}\)
$$\vec m=\gamma\vec\Gamma_0$$

Types de matériaux magnétique

Types de matériaux magnétique

• Diamagnétiques: \(\chi_m\lt 0\) et \(|\chi_m|\lt \lt 1\quad (\approx 10^{-5})\)

Exemple: \(C\), \({{Cv}}\), \(Ag\)

• Paramagnétiques : \(\chi_m\gt 0\) et \(\chi_m\lt \lt 1\quad (\approx 10^{-4})\)

Exemple: \(Mg\), \({{Al}}\)

• Ferromagnétiques: \(\chi_m\gt 0\) et \(|\chi_m|\gt \gt 1\quad (\approx 50)\) à \(10^5\)

Exemple: \(Fe\), \({{Co}}\), \(N\)
Diamagnétisme
Paramagnétisme
Ferromagnétisme